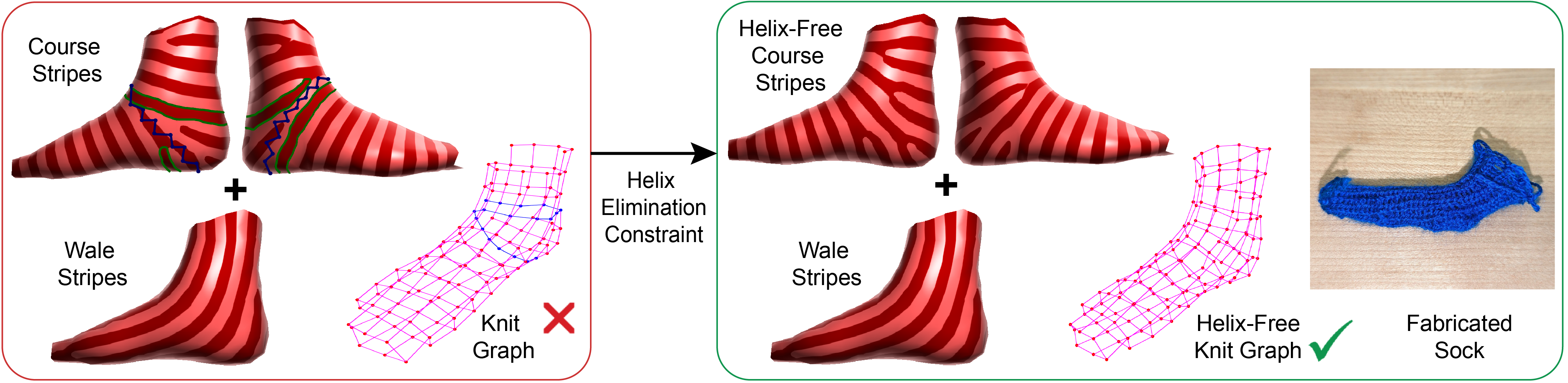
The problem of placing evenly-spaced stripes on a triangular mesh mirrors that of having evenly-spaced course rows and wale columns in a knit graph for a given geometry. This work presents strategies for producing helix-free stripe patterns and traces them to produce helix-free knit graphs suitable for machine knitting. We optimize directly for the discrete differential (1-form) of the stripe texture function, i.e., the spinning form, and demonstrate the knitting-specific advantages of this framework. In particular, we note how simple linear constraints allow us to place stitch irregularities, align course rows and wale columns to boundary/feature curves, and eliminate helical stripes. Two mixed-integer optimization strategies using these constraints are presented and applied to several mesh models. The results are smooth, globally-informed, helix-free stripe patterns that we trace to produce machine-knittable graphs. We further provide an explicit characterization of helical stripes and a theoretical analysis of their elimination constraints.
@inproceedings{mitra2023helix,
title={Helix-Free Stripes for Knit Graph Design},
author={Mitra, Rahul and Makatura, Liane and Whiting, Emily and Chien, Edward},
booktitle={ACM SIGGRAPH 2023 Conference Proceedings},
pages={1--9},
year={2023}
}